对数和函数是数学中的重要概念，广泛应用于科学计算、统计学、工程学等领域，本文将围绕对数和函数的基本概念、性质、应用以及实例进行详细阐述，帮助读者更深入地理解这一专题。

对数的概念及性质

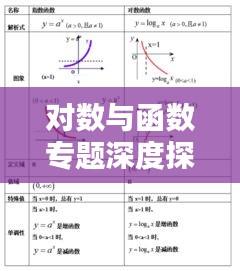
1、对数的定义：对数是一种表示数字的方法，以幂的形式表示数的关系，以10为底的对数表示为lgN，表示10的多少次方等于N。

2、对数的性质：对数具有许多重要的性质，如正值性、单调性、换底公式等，这些性质为对数和函数的研究提供了基础。

对数函数的概念及性质

1、对数函数定义：对数函数是一种特殊的函数，以自变量值的对数作为函数的值，常见的对数函数包括自然对数函数和对数底为10的对数函数等。

2、对数函数的性质：对数函数具有单调性、奇偶性、有界性等性质，这些性质有助于我们更好地理解和应用对数函数。

对数和函数的应用

对数和函数在数学及实际应用中具有广泛的应用，在解决复利问题、音响工程中的分贝计算、生物学中的pH值计算等方面，对数和函数发挥着重要作用，对数和函数也在统计学、金融、物理学等领域有着广泛的应用。

实例解析

1、复利问题：通过应用对数函数，可以方便地求解一定期限内的复利问题，如计算存款的本息总和等。

2、分贝计算：在音响工程中，通过对数和函数的运算，可以将声音的强度转换为分贝值，以便进行声音的比较和分析。

3、pH值计算：在生物学中，通过对数运算可以方便地计算溶液的pH值，从而了解溶液的酸碱性质。

对数和函数的深入探究

除了基本概念和应用外，对数和函数还有许多值得深入探究的内容，对数函数的图像与性质之间的关系、对数运算的精度问题、对数函数的近似计算等，这些内容为对数和函数的研究提供了更深入的视角，有助于我们更全面地理解这一专题。

对数和函数是数学中的重要概念，具有广泛的应用价值，本文详细阐述了对数和函数的基本概念、性质、应用以及实例，希望能够帮助读者更深入地理解这一专题，为了更好地掌握对数和函数，读者还需要通过实践来加深对相关知识的理解和掌握，以便更好地应用于实际问题的解决。

建议与展望

1、建议：读者可以通过练习大量的题目来加深对数和对数函数的理解，同时可以尝试将所学知识应用于实际问题的解决，还可以阅读相关教材、参考书籍和在线资源，以获取更全面的知识。

2、展望：随着科技的发展，对数和函数的应用将更加广泛，在人工智能、大数据分析等领域，对数和函数将发挥更加重要的作用，希望读者能够持续关注这一专题的最新发展，以便更好地应用所学知识。

对数和函数是数学中的重要专题，具有广泛的应用价值，本文旨在帮助读者更深入地理解这一专题，希望读者能够通过不断学习和实践，更好地掌握对数和函数的相关知识。